Elsa Ibanez

The Reshetikhin-Turaev 3-manifold invariants motivate various research subjects in low-dimensional quantum topology : effective constructions by quantum groups theory, effective constructions by colored skein modules, extensions in TQFT, mapping class group representations. The first eponym construction was given in 1991 in [RT91] and rests on two main tools. The first one is surgery which allow to replace oriented compact 3-manifold study with ribbon links in the 3-sphere. The second tool is the notable structure of finite dimensional representations category associated to quantum groups U_q(g) where g is a Lie algebra and q a root of unity.

 

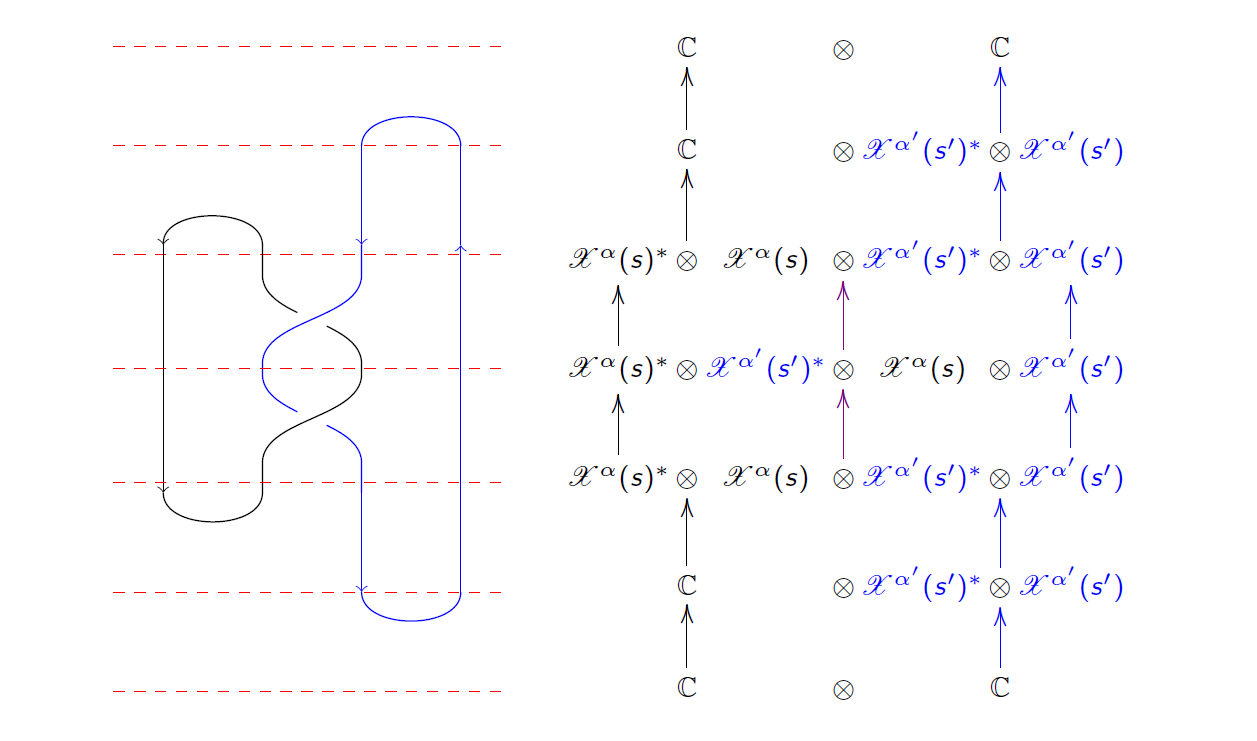
Fundamental examples of these categories are provided by quotient quantum groups U_q(sl2) associated to the Lie algebra sl2 and roots of unity q. Their finite dimensional representations categories Rep^{fd}_q have a natural tensor product and duality. In accordance with Krull-Schmidt theorem, for all root of unity q, the objects of Rep^{fg}_q decompose into finite direct sum of indecomposable modules up to isomorphisms. Among them, Reshetikhin and Turaev use only the simple ones. They obtain thus a modular category whose objects are semi-simple, generated by a finite number of simple modules {X_1^q,...,X_N^q} up to isomorphisms, with non-zero quantum traces (see [RT91, § 3). Then they construct their invariants with these modules and traces, which one can be extended naturally in TQFT (see [RT91, § 4]). In this way, Reshetikhin and Turaev associate to every cobordism (M,Sigma,Sigma') a functor F : (Sigma,M) -> (V_q(Sigma),f_q(M)), and to every connected oriented closed surface a projective representation phi -> f_g(Sigma x_phi [0,1]) (see [RT91, § 4.6]).

​

In the articles [Lic91], [Lic92] et [Lic93], Lickorish offers an alternative topological constructions of these quantum invariants for sl2. Skein modules stand in for finite dimensional representations, and Jones-Wenzl idempotents {f_1^q,...,f_N^q} with non-zero traces (see [Lic92, § 2, § 4]) for simple modules. He finds the [RT91]-invariants again for even roots of unity, and the categories provided by links colored with Jones-Wenzl idempotents turn out to have a similar structure than [RT91]-modular categories. Based on this observation, Blanchet,Habegger, Masbaum and Vogel generalized the Lickorish's work for all roots of unity in [BHMV92], and they extended their invariants into TQFT in [BHMV95]. Like this, they obtain projective representations of mapping class group on skein modules.

​

In this area, I am mainly interested by :

• the finite dimensional representations category associated to the restricted quantum group U_q(sl2), where q is a primitive even root of unity,

• the colored skein module associated to the torus, with special idempotents and nilpotents as a system of colors,

• the linear projective mapping class group representations, specifically in the torus (with a hole) case.

​

References :

[BHMV92] C. Blanchet, N. Habegger, G. Masbaum et P. Vogel : Three-manifold invariants derived from the Kauffman bracket. Topology, 31(4):685–699, 1992.

[BHMV95] C. Blanchet, N. Habegger, G. Masbaum et P. Vogel : TQFTs derived from the Kauffman bracket. Topology, 34(4):883–927, 1995.

[CFS95] J. S. Carter, D. E. Flath et M. Saito : The classical and quantum 6j-symbols. Princeton University Press, 1995.

[CGPM14] F. Costantino, N. Geer et B. Patureau-Mirand : Quantum invariants of 3-manifolds via link surgery presentations and non-semi-simple categories. Journal of Topology, 7(4):1005–1053, 2014.

[FGST06] B. L. Feigin, A. M. Gainutdinov, A. M. Semikhanov et I. Yu. Tipunin : Modular group representation and fusion in logarithmic CFTs and in the quantum group center. Communications in Mathematical Physics, 265(1):47–93, 2006.

[GPMT09] N. Geer, B. Patureau-Mirand et V. Turaev : Modified quantum dimensions and re-normalized link invariants. Compositio Mathematica, 145:196–212, 2009.

[Lic91] W. B. R. Lickorish : Three-manifolds and the Temperley-lieb algebra. Mathematische Annalen, 290:657–670, 1991.

[Lic92] W. B. R. Lickorish : Calculations with the Temperley-Lieb algebra. Commentarii Mathematici Helvetici, 67(1):571–591, 1992.

[Lic93] W. B. R. Lickorish : Skeins and handelbodies. Pacific Journal of Mathematics, 159(2):337–349, 1993.

[LM94] V. Lyubashenko et S. Majid : Braided groups and quantum Fourier transform. Journal of Algebra, 166:506–528, 1994.

[RT91] N. Reshetikhin et V. G. Turaev : Invariants of 3-manifolds via link polynomials and quantum groups. Inventiones Mathematicae, 103(3):547–597, 1991.